Como fazer Interpolação de Dados Geoespaciais e sua Representação em Mapa usando a Linguagem R

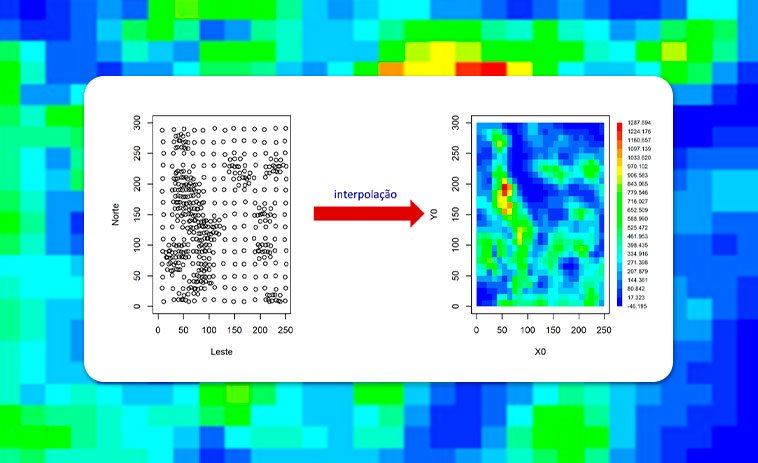
Neste artigo, iremos mostrar como se pode fazer a interpolação de dados geoespaciais e sua representação em mapa como ilustra a figura abaixo.

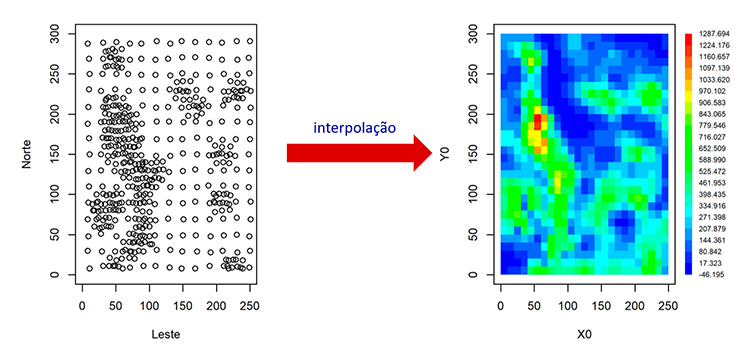
Obs.: Os arquivos utilizados, assim como o script estão detalhados no final desse artigo, assim como nesse link.

Isaaks e Srivastava (1989, p. 4-9) proporcionam o conjunto de dados walker.dat que representa uma amostra com 470 pontos. Estes pontos foram extraídos de um conjunto completo (população) com 78000 pontos em uma malha regular de 260 por 300 nós. Na realidade, os dados do modelo digital de terreno da região do Lago Walker são transformados para as variáveis V e U que representam teores simulados em ppm (walker_dat.csv). Nesta demonstração, vamos usar os dados da variável V. Esses dados estão salvos no arquivo walker_dat.csv, que contém seis variáveis: ID, Xlocation, Ylocation, V, U e T, onde V e U são expressos em ppm e T é uma variável indicadora.
Para obtenção de um mapa como mostrado na Figura 1, deve-se definir o tipo de malha regular sobre os nós ou nos centros (Figura 2).

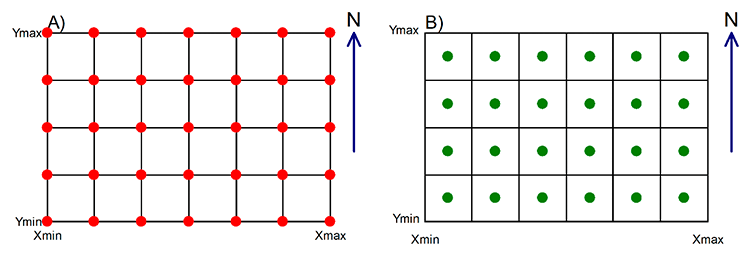
O próximo passo consiste na escolha do método de interpolação de dados 2D, que pode ser global ou local (Figura 3).

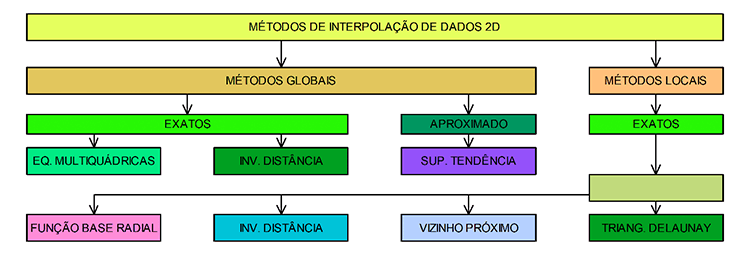
Neste caso, escolhemos o método das equações multiquádricas globais propostas originalmente por Hardy (1971, p. 1906). A forma geral da equação multiquádrica em 2D, segundo Hardy (1971, p. 1906):

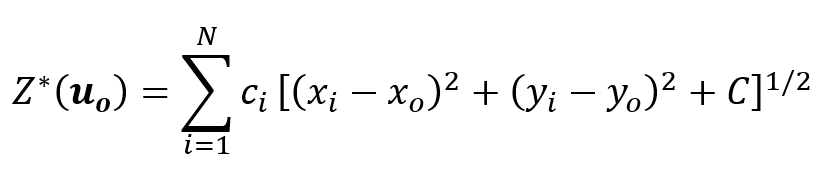
Onde os coeficientes {c_i,i=1,N} são determinados pela resolução de um sistema de equações lineares (Hardy, 1971, p. 1907):

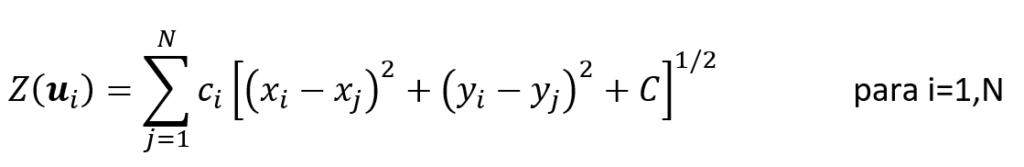
Trata-se em resolver o sistema de equações lineares:

Em forma matricial, tem-se:

Onde

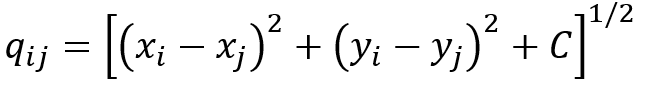
C é uma constante positiva e, segundo Franke (1982, p. 191), o método é bastante estável com relação à essa constante dando, consistentemente, bons resultados. Caso seja de interesse do Leitor, a teoria e aplicações da interpolação multiquádrica pode ser encontrada em Yamamoto (2020, p. 157-163).
O desafio é obter em 10 passos o mapa mostrado na Figura 1, por meio de scripts na linguagem R. O script completo (emqGlobal.R) pode ser baixado diretamente do site geokrigagem.com.br. Assim, vamos demonstrar passo a passo a geração do mapa da Figura 1. Os scripts a seguir podem ser representados em três cores: vermelha – linha executada no console, azul – resultado mostrado no console e preta – linha de comando no editor de scripts da linguagem R.

Passo 1 – Leitura dos dados de entrada e arquivo de parâmetros

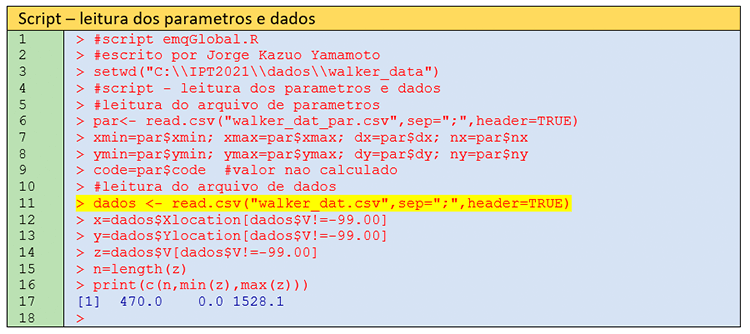
A linha 3 informa o diretório no qual estarão os dados de entrada e o arquivo de parâmetros. Caso o Leitor queira executar esse script, há necessidade de se informar o diretório correto por meio do comando setwd(). Basta colar entre aspas duplas o diretório copiado no Windows explorer e observando que há necessidade de se duplicar as barras invertidas.
Na linha 6, faz-se a leitura do arquivo de parâmetros (walker_dat_par.csv), que contém os parâmetros da malha regular (Figura 4).

Este arquivo contempla os parâmetros a serem aplicados para os eixos X e Y. Além disso, define-se um valor -999 para code, que é usado para casos em que o ponto (nó ou centro da célula) não foi interpolado. Na linha 12, tem-se a leitura do arquivo de entrada. Nas linhas 12-14, os objetos x, y e z são criados, mas com a restrição que os dados de V sejam diferentes de -99 (dado V ausente). Não é exatamente o caso desse arquivo, mas se fossemos trabalhar com a variável U haveria necessidade de um comando equivalente para esta variável, uma vez que sua amostragem não engloba toda a região. Os resultados da leitura dos dados estão mostrados na linha 17, que são 470 pontos de dados e os valores mínimo e máximo da variável V (0 – 1528,1).

Passo 2 – Montagem e resolução do sistema de equações lineares

A linha 3 define um objeto do tipo “matrix”, com n linhas por n colunas. A matriz dos coeficientes (equação 4) é calculada nas linhas 5-7. O vetor do lado direito é definido na linha 8. A linha 9 resolve o sistema linear de equações com base na função solve() da biblioteca padrão do R. Esta função pertence à biblioteca de rotinas de álgebra linear LAPACK e, portanto, extremamente confiável.

Passo 3 – Interpolação da malha regular

Neste script, a malha regular é interpolada, a partir dos parâmetros lidos do arquivo de parâmetros (walker_dat_par.csv). Este Autor convenciona usar as variáveis i e j para referenciar as coordenadas Y e X, respectivamente. Em apenas 10 linhas fazemos a interpolação de uma malha regular. A linha 3 gera os objetos x0, y0 e z0. Os dois primeiros irão armazenar as coordenadas X e Y. O terceiro serve para guardar o valor interpolado nas coordenadas (x0, y0). Observe-se que nas linhas 10-11, aplica-se a equação (1).

Passo 4 – Gravação do arquivo csv da malha regular

Neste passo, vamos gravar o arquivo da malha regular. Para isso, geramos um data frame (linha 2), conforme os nomes atribuídos nas linhas 3-5. A linha 6 direciona a gravação para um diretório predefinido. Solicita-se ao Leitor adequar o script para o diretório de seu computador. A gravação propriamente dita é feita na linha 7, sem a identificação das linhas e sem aspas duplas nos valores.

Passo 5 – Leitura do arquivo de cores

A partir do Passo 5, vamos proceder como se fosse um script separado para fazer a representação gráfica, ou seja, a malha regular já foi interpolada e gravada em arquivo csv.
A linha 3 define o diretório no qual se encontra o arquivo cores.csv. Pede-se ao Leitor abrir esse arquivo em bloco de notas do tipo Notepad++. Poderia abrir no Excel, mas desde que a configuração regional estivesse definida com o separador decimal como ponto ao invés de vírgula. Ao abrir o arquivo, o Leitor irá verificar que os valores de R, G e B variam de zero a um. Isso porque no R, esses valores são normalizados. Para verificar os valores reais, basta multiplicar por 255.

Passo 6 – Leitura dos arquivos de parâmetros e da malha regular

O único comentário que precisamos fazer neste script (linha 10) é com relação ao separador que é a vírgula, pois o arquivo walker_dat_EMQ.csv foi gerado pelo R. Lembrando que a especificação incorreta do separador leva a erros inesperados na execução do script.

Passo 7 – Definição da dimensão do mapa no dispositivo gráfico novo

Os objetos cx e cy se destinam à definição das dimensões do mapa nos eixos X e Y, mantendo a proporcionalidade. Na linha 9, define-se um novo dispositivo gráfico com os valores calculados anteriormente (cx e cy) em polegadas. As linhas 11-12 estabelecem o dispositivo gráfico como sendo do tipo jpeg, com resolução de 300 pontos por polegada. Nas linhas 14-15, gera-se uma área de plotagem em branco, que irá receber o mapa imagem com a representação dos resultados da interpolação multiquádrica. A área de plotagem terá dimensões proporcionais a cx e cy.

Passo 8 – Definição dos limites (zmin, zmax) para representação em mapa imagem

Esse script poderia se resumir apenas à linha 2, mas para fins didáticos se mostra as linhas 5 até 11, que têm o mesmo efeito da linha 2. A programação feita na linha 2 reflete a natureza orientada a objetos da linguagem R. Os limites são usados para representação do mapa imagem em termos das cores predefinidas anteriormente (Passo 5).

Passo 9 – Plotagem dos retângulos do mapa imagem

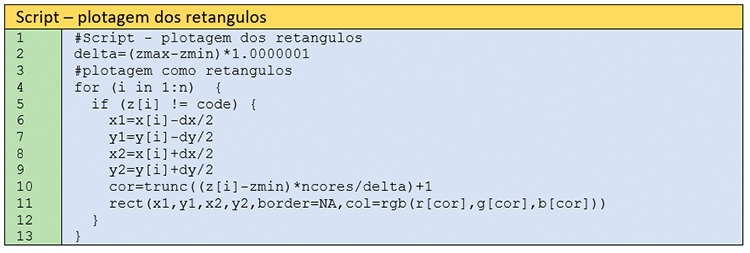
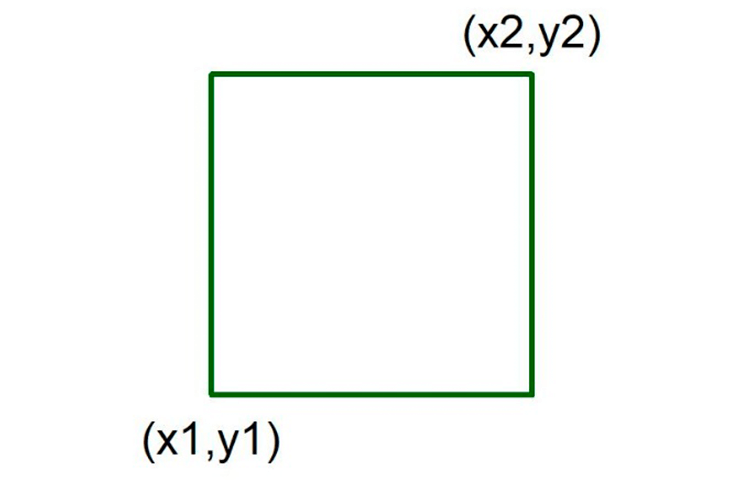
A representação em mapa imagem é feita por meio da plotagem de retângulos, os quais são definidos pelas coordenadas do canto inferior esquerdo e do canto superior direito (Figura 5). Agora, n se refere ao número de nós da malha regular, conforme sua leitura feita na linha 12 do Passo 6. As linhas 6-9 calculam as coordenadas necessárias para representação do retângulo (Figura 5). A cor é calculada como uma função que retorna valores sempre entre 1 e ncores. A variável delta que é a diferença entre zmax e zmin multiplicada por um valor muito próximo de 1, garante que sempre a cor irá variar entre 1 e ncores. Finalmente, na linha 11, faz-se a plotagem do retângulo.

Passo 10 – Plotagem da legenda de cores

O último passo se refere à plotagem da legenda de cores, que é feita também como retângulos com os valores variando entre zmin e zmax. Verifique-se que toda a legenda é parametrizada em função dos limites do mapa. Os objetos eixox e eixoy armazenam (ncores+1) valores referentes às coordenadas x e y dentro da área de plotagem. Da mesma forma, vetorz armazena os valores da variável de interesse divididos em (ncores+1) intervalos. Na linha 14, os valores da variável de interesse são plotados nas coordenadas eixox e eixoy, respectivamente. Por fim, os retângulos são plotados nas linhas 15-16.

Resultado

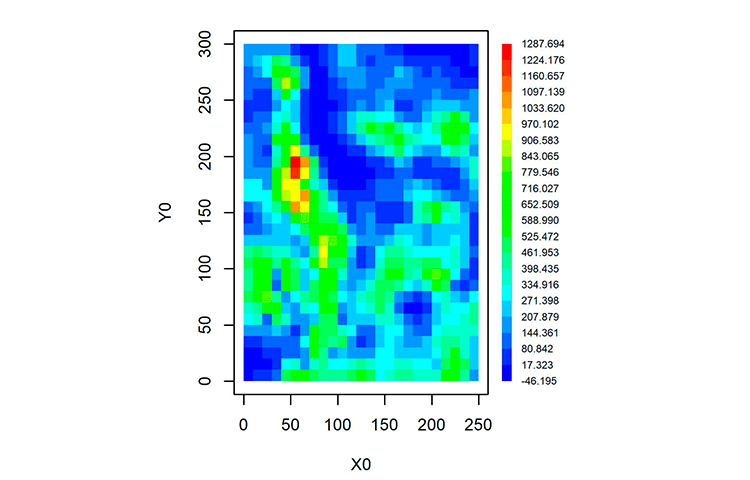
O resultado da execução do script completo pode ser visualizado na Figura 6.

Discussão

O resultado obtido mostra um ajuste respeitando as feições topográficas dos dados originais. Porém, deve-se comentar que o limite inferior negativo -46,195 era indesejável. Esse valor ocorre devido à resolução de um sistema de grandes dimensões 470 X 470, que pode ocasionar erros de arredondamento e truncamento. Esse efeito pode ser verificado no arquivo a seguir (Figura 7), onde calculamos os valores sobre os pontos de dados. Conclui-se que o ajuste pode ser considerado exato (passando pelos pontos), mas os pequenos resíduos se acumulam e se propagam. Entretanto, quando o número de pontos de dados for menor, o método das equações multiquádricas globais dá sempre um excelente resultado. Evidentemente, no caso com grande quantidade de pontos se pode aplicar outros métodos exatos como, por exemplo, funções de base radial ou triangulação de Delaunay.

Considerações finais

Este artigo demonstrou uma aplicação prática da interpolação multiquádrica global para dados geoespaciais. Evidentemente, existem outros métodos de interpolação, incluindo a krigagem ordinária. Se o Leitor estiver interessado em detalhes da metodologia empregada na interpolação multiquádrica e nos demais métodos de interpolação, sugere-se a seguinte referência: Yamamoto (2020). Esta publicação contempla não apenas a teoria, mas também os scripts correspondentes em linguagem R.

Informação relevante

Este artigo foi baseado em uma apresentação feita no canal YouTube Geocast Brasil no dia 13 de abril de 2021.

Agradecimentos

O Autor expressa seus agradecimentos aos organizadores do canal YouTube Geocast Brasil que possibilitou a apresentação da qual foi derivada este artigo.

Referências bibliográficas

Franke, R. 1982. Scattered data interpolation: test of some methods. Math. of Computation. V. 38, p. 181-200.

Hardy, R.L. 1971. Multiquadric equations of topography and other irregular surfaces. J. Geophysical Research, V. 76, p. 1905-1915.

Isaaks, E.H.; Srivastava, R.M. 1989, Applied geostatistics, New York, Oxford University Press. 561p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 344p.

Arquivos de dados e script

Para executar o script fornecido (emqGloba.R) será necessário adequar os diretórios de entrada e saída, conforme os comandos setwd(). Os seguintes arquivos precisam estar nos diretórios indicados, se o Leitor desejar executar sem alterações significativas.

Diretório: C:\IPT2021\dados\walker_data
Dados: walker_dat.csv e walker_dat_par.csv

Diretório: C:\IPT2021\dados\cores
Dados: cores.csv

Diretório: C:\IPT2021\dados\figuras

Quer aprender programação em linguagem R?

Se você gostaria de aprender mais sobre a Linguagem R ou dar seus primeiros passos nesse universo, temos um curso on-line e um livro para oferecer:

Curso online R na Prática

Livro Estatística, análise e Interpolação de Dados Geoespaciais