Como Calcular o Índice Moran – Autocorrelação Espacial

O índice de Moran é comumente utilizado como medida da autocorrelação espacial para dados contínuos, de acordo com a seguinte expressão (Burt et al. 2009, p. 554):

Onde n é o número de pontos de dados, X é a variável aleatória contínua e w_ij são os elementos da matriz W dos pesos espaciais que representa a relação geográfica entre todos os pares de pontos, segundo os autores mencionados.

Burt et al. (2009, p. 554-555) mencionam uma simplificação da expressão (1) a partir da normalização dos pesos por linha, que será considerada no cálculo do índice de Moran.

Este índice pode ser usado para verificar se os dados amostrais apresentam autocorrelação espacial na área toda, ou seja, em termos globais. Por outro lado, quando se calcula para subconjuntos de dados separados por uma distância (lag), tem-se o índice de Moran aplicado localmente. Geralmente, os resultados dos índices de Moran são representados graficamente contra a distância resultando em um correlograma espacial (e.g. Fortin et al. 2002, p. 4-5; Huo et al. 2012, p. 999)

Em termos globais, deseja-se saber se os dados amostrais apresentam autocorrelação espacial. Assim, formula-se as seguintes hipóteses:

Sob a hipótese nula, a média e a variância da distribuição amostral de I são calculados de acordo com as seguintes expressões (Gittleman e Kot, 1990, p. 230):

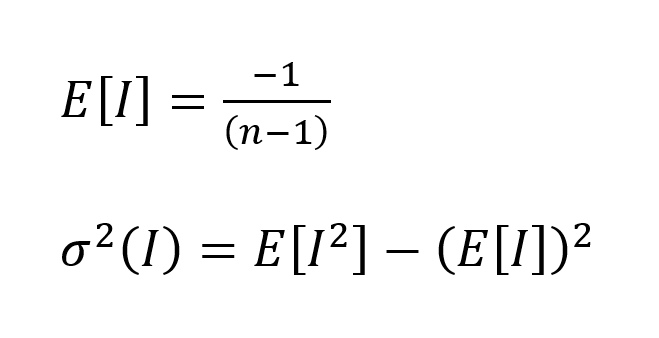
A fórmula da variância envolve o cálculo da esperança matemática dos valores de I ao quadrado, que pode ser descrita simplificadamente como (https://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-statistics-toolbox/h-global-morans-i-additional-math.htm, consultado em 06/11/2020 ):

Para determinação dos termos A, B e C, calcula-se as seguintes quantidades (site mencionado anteriormente e Gittleman e Kot, 1990, p. 230):

                Dessa forma, pode-se calcular os termos A, B e C:

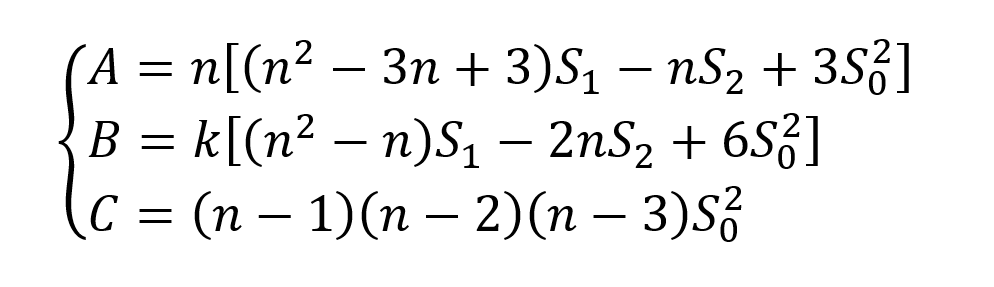
O índice Moran global pode ser padronizado para escores da distribuição normal (Huo et al. 2012, p. 998):

                                                                                                                                   (7)

O escore calculado (6) permite fazer a localização de ponto na curva da distribuição normal. A partir deste ponto (até o infinito), pode-se calcular a área sob a curva normal para determinação do valor-p. Nesse caso, o teste de hipóteses é bicaudal e, portanto, a área encontrada é multiplicada por 2. Na linguagem R, o comando para se calcular o valor-p é simplesmente: valor_p=2(1-pnorm(Z))

Tendo em vista o exposto, pode-se desenvolver um script em R e não simplesmente usar um pacote da biblioteca do R, haja vista o objetivo didático desta publicação, que é fazer a conexão entre a teoria e a prática.

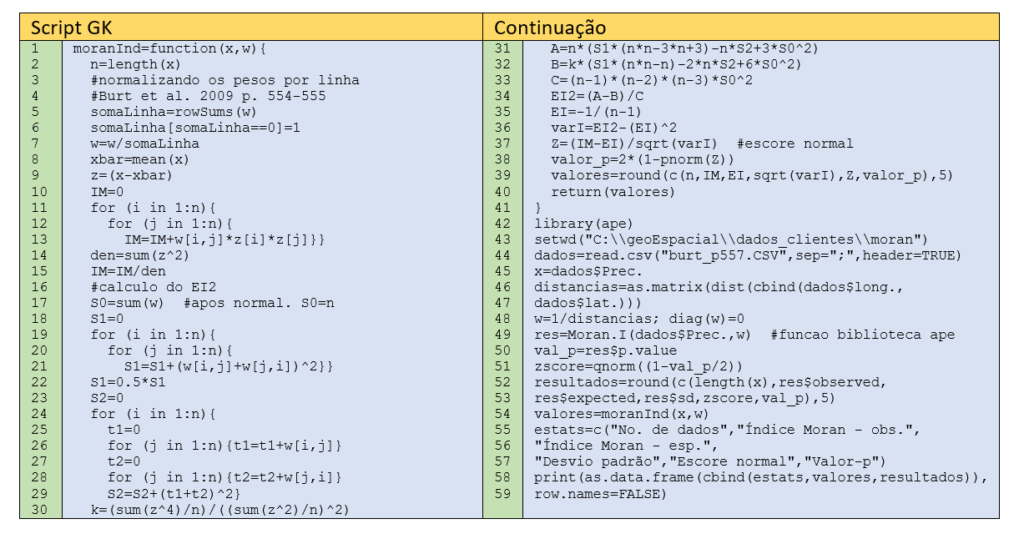
A função moranInd() recebe os objetos x e w (linha 1) e retorna o vetor de resultados denominado valores (linha 40). Nas linhas 5-7, faz-se a normalização dos pesos, sabendo que após a normalização a soma dos pesos é igual a n (número de dados). O objeto x é transformado em outro chamado z, que é o resultado de x subtraído da média (linha 9).

O índice de Moran é calculado nas linhas 10-15, conforme a equação (1). Prosseguindo, calcula-se os valores constantes em (5), entre as linhas 17-30. Feito isso, calcula-se as variáveis auxiliares (6), de acordo com as linhas 31-33. Na linha 34, determina-se a média dos valores de I ao quadrado, com base na relação (4).

O valor esperado de I é calculado na linha 35. Assim, pode-se computar a variância de I na linha 36. Com esses elementos, pode-se obter o escore Z (linha 37) da distribuição normal. O valor-p é o resultado da área da distribuição normal entre Z e o infinito (linha 38), por meio da função pnorm().

Para uma aplicação, vamos considerar os dados de precipitação no Estado da Califórnia (EUA), conforme observações feitas em 30 estações (Burt et al. 2009, p. 556-557). O objetivo é verificar os dados de precipitação apresentam autocorrelação espacial (H₀) ou se os dados distribuídos aleatoriamente naquele estado (H₁).

No Script GK, a leitura dos dados é feita na linha 44, em seguida o objeto x recebe os dados de precipitação (linha 45). Nas linhas 46-48, calcula-se a matriz W dos pesos. Nesse caso, usa-se distâncias Euclideanas, por meio da função dist().

Os pesos são determinados como o inverso da distância, conforme a linha 48, que também inclui o comando para deixar a matriz W com a diagonal nula. Na linha 49, chama-se a função Moran.I() do pacote “ape”, que faz os cálculos da autocorrelação espacial. Na linha 51, determina-se o escore normal correspondente ao valor-p (linha 50).

Os resultados da execução do Script GK se encontram a seguir:

Como se pode verificar, os resultados entre os dois procedimentos foram absolutamente iguais. Em relação ao teste de hipóteses, pode-se afirmar categoricamente que os dados de precipitação apresentam autocorrelação espacial, pois como o valor-p é menor que 0,05 (nível de significância) se rejeita a hipótese nula e se aceita a hipótese alternativa.

Referências bibliográficas

Burt, J.E.; Barber, G.M.; Rigby, D.L. 2009. Elementary statistics for geographers. New York, The Guilford Press. 653p.

Fortin, M.J.; Dale, M.R.T.; Hoef, J. 2002, Spatial analysis in ecology. In: Shaarawi e Piegorsch, Encyclopedia of Environmetrics, vol. 4, p. 2051-2058.

Gittleman, J.L.; Kot, M. 1990. Adaptation: statistics and a null model for estimating phylogenetic effects. Syst. Zool., Vo. 39, p. 227-241.

Huo, X.N.; Li, H.; Sun, D.F.; Zhou, L.D.; Li, B.G. 2012. Combining geostatistics with Moran’s I analysis for mapping soil heavy metals in Beijing, China. Int. J. Environ. Res. Public Health, Vol. 9, p. 995-1017.

Próximo artigo

O próximo artigo irá abordar o cálculo do índice Moran e fazer a comparação com a função variograma.

Confira também mais artigos como esse clicando aqui