Retrospectiva da Geoestatística II: Teoria das Variáveis Regionalizadas e Suas Aplicações

O resumo da Retrospectiva da Geoestatística de hoje é sobre A Teoria das Variáveis Regionalizadas e Suas Aplicações (The Theory of Regionalized Variables and its Applications, 1971). 

A Teoria das Variáveis Regionalizadas e Suas Aplicações foi publicada em 1971, por Matheron. É dividida em cinco capítulos: 0) Introdução; 1) Métodos transitivos; 2) Teoria das funções aleatórias intrínsecas; 3) Krigagem; 4) Krigagem Universal.

No Capítulo 0, o autor revisa os conceitos de cálculo integral e apresenta a operação de convolução, que tem um papel importante em geoestatística à medida que tem conexão com o processo da média móvel¹. Segundo esse autor, a convolução de duas funções f1(x) e f2(x) é uma função g(x):

Ainda nesta introdução, Matheron (1971, p. 5)  define geoestatística como a aplicação da teoria das variáveis regionalizadas para a estimativa de depósitos minerais, com todas as suas implicações. Além disso, ele estabelece o conceito de regionalização como sendo associado a um fenômeno que se distribui no espaço e exibe uma certa estrutura. Assim, a variável regionalizada foi definida matematicamente como uma função f(x) no ponto (x), mas geralmente uma função muito irregular, que mostra dois aspectos contraditórios: aspecto aleatório, caracterizada por uma irregularidade marcante e variações imprevisíveis de um ponto a outro; aspecto estruturado, que deve refletir em alguma extensão as características estruturais do fenômeno regionalizado.

 

Ainda segundo esse autor, a “Teoria das variáveis regionalizadas” tem dois objetivos principais: em base teórica, expressar as propriedades estruturais em uma forma adequada; e em base prática, resolver o problema da estimativa de uma variável regionalizada a partir de dados amostrais.

 

Fenômeno de transição

No primeiro capítulo, o autor exemplifica um fenômeno de transição, como aquele que pode ou não apresentar uma característica, como, por exemplo, uma formação geológica S de extensão limitada, em que uma sondagem pode ou não perfurá-la. Essa situação pode ser expressa pela função indicadora de S, como (Matheron, 1971, p. 9):

 

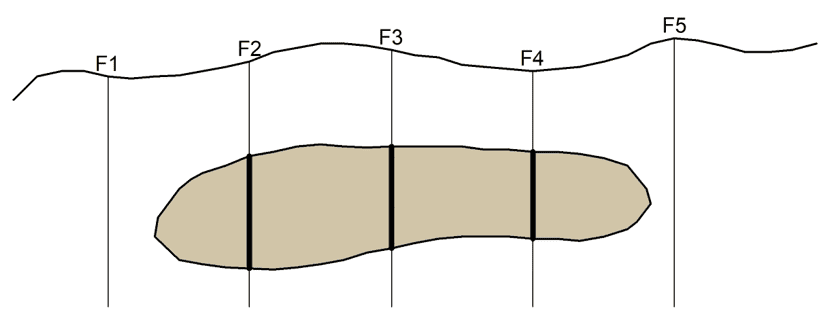
Interessante observar que o conceito da função indicadora surge com Matheron. Na realidade, segundo Matheron (1971, p. 9), o interesse está na fronteira de S, onde k(x) pode variar, pois dentro é um e fora é zero. Daí surge o nome de fenômeno de transição. Assim, continuando o desenvolvimento, seja f(x) uma variável regionalizada que é zero fora do campo, então o covariograma transitivo g(h) pode ser definido como (Matheron, 1971, p. 11):

Trata-se de uma formulação importante, pois a equação (2) é o fundamento da geoestatística, como se conhece atualmente.

 

Apresentação da função aleatória

Outra importante definição é dada no Capítulo 2, no qual o autor apresenta a noção de uma função aleatória. Seja uma sequência de k variáveis aleatórias Y1, Y2, …, Yk que define um vetor aleatório Y=(Y1, Y2, …, Yk) com k componentes. Quando k tende ao infinito, então se tem uma função aleatória (Matheron, 1971, p. 50). Assim, segundo esse autor, uma realização y(x) de uma função aleatória Y(x) pode sempre ser considerada como uma variável regionalizada. Reciprocamente, uma dada variável regionalizada y(x) pode ser considerada como a realização de uma certa função aleatória Y(x). Essa interpretação torna possível a aplicação da teoria da probabilidade das funções aleatórias para as variáveis regionalizadas⁸

Em seguida, Matheron estabelece as definições da função aleatória Y(x): estacionaridade, esperança, covariância, estacionaridade de segunda ordem, variância à priori infinita e hipótese intrínseca.

Além disso, o autor define outras propriedades do variograma: continuidade, comportamento na origem, efeito pepita, amplitude e anisotropias (Matheron, 1971, p. 57-58). Com relação ao efeito pepita, a função variograma exibe um rápido crescimento dentro de uma dimensão a (que é um valor infinitesimalmente pequeno). Isso é visível no desenho esquemático da Figura 3 (Matheron, 1971, p. 77)..

 

A variância de extensão, segundo Matheron (1971, p. 64)P, é a variância do erro Z(v’)-Z(v) que se comete pela atribuição em v’, o teor médio Z(v) de v:

Krigagem – Encontrando o melhor estimador possível

O Capítulo 3 se intitula “Krigagem”, cujo termo significa encontrar o melhor estimador possível do teor de um painel, levando em conta toda a informação disponível, tanto fora como dentro desse painel (Matheron, 1971, p. 115). 

Matheron ressalta que o aspecto prático mais importante da krigagem não é o fato de proporcionar a melhor estimativa possível, mas que em adição evita quaisquer erros sistemáticos. Matheron (1971, p. 123-126) faz todo o desenvolvimento matemático das equações de krigagem ordinária, bem como a estimativa ótima da média local.

A Krigagem universal

No Capítulo 4, o autor desenvolve a krigagem universal. Seu objetivo é estabelecer, em termos de funções aleatórias não estacionárias, a estimativa da componente de tendência. Em seguida, mostra o cálculo do termo de tendência e o desenvolvimento matemático para se chegar às equações de krigagem universal.

Ainda neste capítulo, Matheron (1971, p. 184)  trata da cokrigagem, que permite fazer o estudo e estimativa de várias variáveis regionalizadas simultaneamente. Com relação à krigagem universal, que usa o variograma residual, Matheron (1971, p. 188) aborda a questão da indeterminabilidade desse tipo de variograma. Segundo esse autor, o variograma residual é teoricamente indeterminável, mas afeta somente a variância dos estimadores ótimos e não os estimadores propriamente ditos.

 

 

 

Referências

Matheron, G. 1971. Teoria das Variáveis Regionalizadas e Suas Aplicações. Paris, École Nationale Supérieure des Mines de Paris. 211p.

 

 

 

 

 

Aprenda as aplicações dos conceitos vistos aqui, dentre outros, neste treinamento em Geoestatística: