Método de Triangularização de Gauss – Parte 1

Em continuidade aos artigos publicados pela Geokrigagem, neste vamos mostrar como se resolve um sistema de equações lineares pelo método direto, conhecido como triangularização de Gauss.

Como vimos anteriormente, o sistema de equações lineares pode ser escrito na forma matricial (Press et al. 1989, p. 28):

Onde A é a matriz dos coeficientes, x é o vetor das incógnitas e b é o vetor y.

O método de triangularização de Gauss consiste em zerar os elementos abaixo da diagonal principal da matriz dos coeficientes. O objetivo é deixar o sistema (2) na seguinte forma:

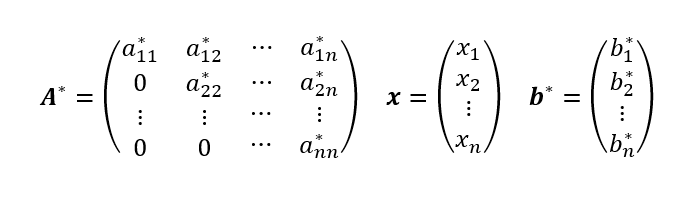
Seja k a linha que contém o elemento da diagonal principal. Define-se o multiplicador como a divisão entre o elemento abaixo da diagonal sobre o elemento que está na diagonal, com o sinal trocado, ou seja, m=-(a[k+1,k]/a[k,k]). Este valor é multiplicado pela linha da diagonal e somado com os elementos da linha abaixo da diagonal. Somando as duas linhas, o elemento abaixo da diagonal principal é zerado. Fazendo isso para todas as linhas abaixo da diagonal principal, tem-se zeros nesta coluna.

O processo é mais bem acompanhado pela solução de um exemplo numérico. Para esse fim, seja o exemplo sugerido por Dunn e Parberry (2011, p. 131), com a permuta de duas linhas que não altera o resultado do sistema linear:

O vetor b é pendurado na matriz A:

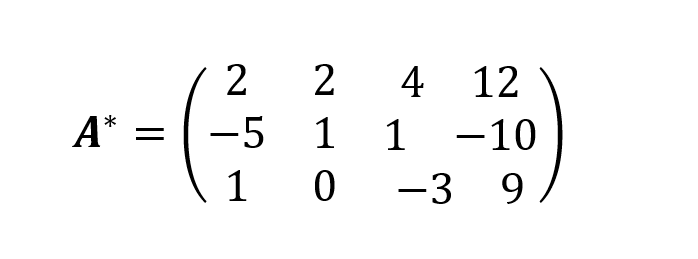
O objetivo é zerar os elementos abaixo da diagonal principal (2, 1 e -3). O primeiro elemento da diagonal principal vale 2. Então, o multiplicador seria m=-(-5/2)=2,5. Mas, esse valor é maior que um, que pode gerar erros de arredondamento quando o sistema for muito grande. Na realidade, verifica-se o módulo do multiplicador que deve ser menor que um. Dessa forma, pode-se permutar a linha que começa com -5 com a linha da diagonal principal que começa com 2. Este procedimento é denominado condensação pivotal. Fazendo isso, o multiplicador é m=0,40 que é multiplicado pelos elementos da linha da diagonal principal e somado com os elementos abaixo da diagonal, como mostra a terceira linha das matrizes do lado direito identificadas como l2 e l3:

Observe-se que a operação é feita com as linhas abaixo da diagonal principal. Após esta multiplicação e soma, o sistema fica:

Há ainda um elemento abaixo da diagonal (-5) que precisa ser zerado. Calcula-se o multiplicador m=-(-1/-5)=-0.20 que é aplicado sobre os elementos da linha que contém a diagonal e somado com a linha que começa com -1:

Após esta operação, tem-se:

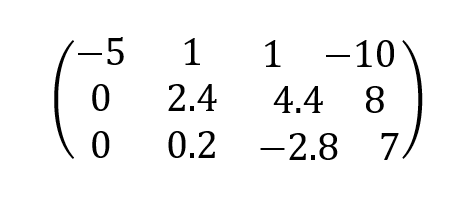
Para completar a triangularização, deve-se zerar o valor 0.2 que aparece abaixo da diagonal 2.4. O multiplicador é –(0.2/2.4)=-0.08333 que é aplicado sobre os elementos da linha em que está a diagonal:

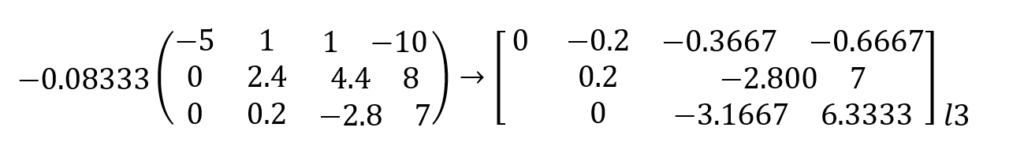
Feito isso, tem-se o sistema triangularizado:

Agora, o sistema de equações lineares pode ser escrito como:

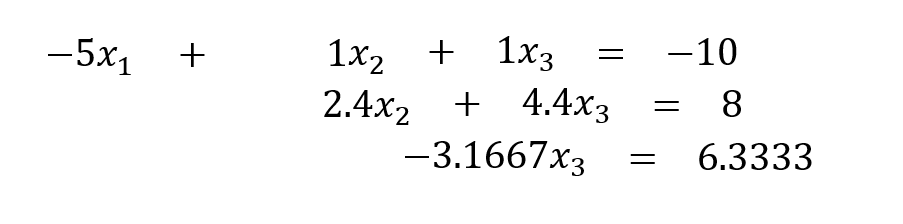
Observe-se que da última equação, pode-se determinar o valor de x₃:

As demais incógnitas são obtidas pelo processo chamado substituição reversa (Press et al. 1989, p. 37):

E, finalmente, tem-se:

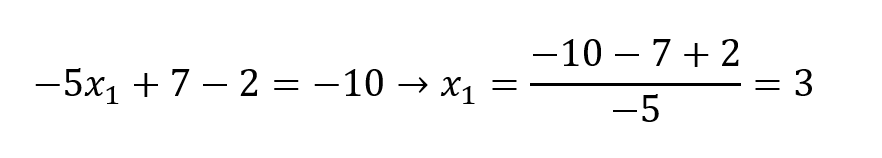
Portanto, o vetor das incógnitas é:

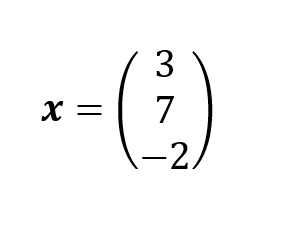
Referências bibliográficas

Dunn, F.; Parberry, I. 2011. 3D Math primer for graphics and game development. Boca Raton, CRC Press. 824p.

Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1989. Numerical recipes in Pascal. New York, Cambridge University Press. 759p.

Próximo artigo

Na sequência, o próximo artigo irá tratar da resolução de sistemas lineares pelo método de triangularização de Gauss, por meio de um script em linguagem R.

Observação: este artigo foi derivado de um capítulo de um livro em preparação:

Yamamoto, J.K. 2020. R na prática. São Paulo, JK Yamamoto-EIRELI.