Algoritmos de Cava Ótima: O Método de Lerchs-Grossmann

Algoritmos de Cava Ótima: O Método de Lerchs Grossmann

Como foi visto no artigo anterior (“O que é Cava Ótima?“), para se obter a Cava Ótima, são necessários muitos cálculos e uso de muitos parâmetros diferentes para chegar a solução. Então o único jeito de se conseguir isso de forma prática é através da iteração de um algoritmo. Para isso, ele deve possuir uma base matemática que garanta que seus resultados sejam a solução ótima.

O Clássico Lerchs Grossmann

Publicado em 1965, o algoritmo de Helmut Lerchs e Ingo Grossmann não tinha condições de ser utilizado na época, devido à baixa capacidade dos computadores. Sua primeira versão comercial foi lançada em 1986 pela Whittle Programming Ltd, programada por Jeff Whittle na linguagem Fortran.

 

Lerchs Grossmann em 2D

Esse algoritmo é baseado na teoria dos grafos. Primeiro, é necessário um Modelo de Blocos, uma matriz com dados da jazida – como teor e densidade em cada bloco – e são necessários parâmetros econômicos para quantificar o valor de cada bloco. A partir do teor e parâmetros econômicos, atribui-se um valor econômico para cada bloco. Em blocos de alto teor, os valores são altos por proporcionarem maior lucro e os blocos de estéril possuem valores negativos por proporcionarem apenas custos de extração. Usaremos a simplificação 2D para facilitar a explicação.

 

Após definir o valor de cada bloco o Modelo de Blocos ficaria assim:

 

 

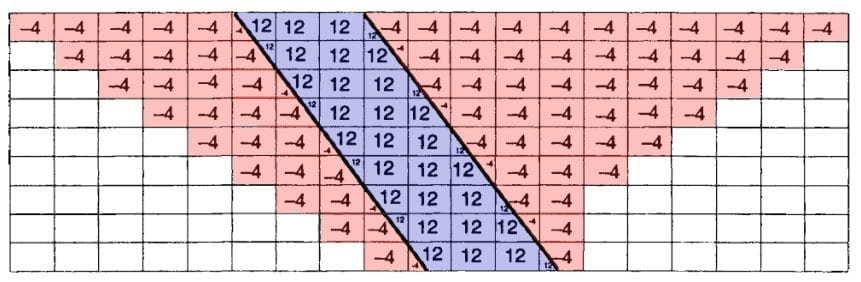
O próximo passo é somar ao valor de cada bloco o valor de todos os blocos que estão acima dele na mesma coluna.

 

 

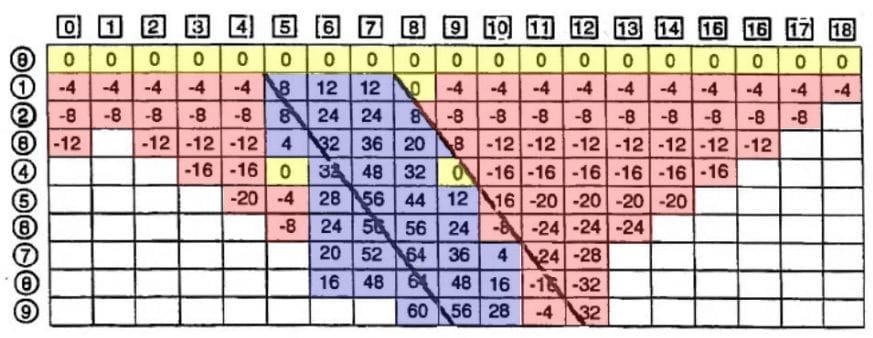
Com esses valores, o algoritmo analisa para cada bloco em qual direção seria mais vantajoso seguir, onde, somando o valor do bloco e do seu vizinho, obtém-se o maior lucro ou menor custo. No caso 2D, ele soma os valores do bloco com os blocos à esquerda, no mesmo nível, no nível inferior e no nível superior, escolhendo o que resultar em uma soma maior:

 

 

Para saber o contorno, é só seguir a partir do bloco da superfície com maior valor – linha 1 e coluna 14 – até atingir a superfície na outra extremidade. Esse caminho é o desenho da Cava Ótima, que gera a maior receita.

 

Lerchs Grossmann em 3D

O caso 3D funciona de forma análoga, porém as restrições estão nas três direções. Portanto, para cada bloco, é preciso analisar a combinação com mais vizinhos.

 

Para 3D, podem ser utilizados dois padrões de restrição, o de 9 blocos ou de 5 blocos. Esses blocos seriam os necessários a serem removidos para cada bloco localizado em um nível mais profundo. Mas esses padrões não geram cavas com ângulos de talude constantes em todas as direções, apenas nas principais – Norte, Sul, Leste e Oeste. Nas outras direções, o ângulo fica maior, no caso do método de 5 blocos, ou menor, no caso de 9 blocos.

Outro problema encontrado é que o ângulo de talude só pode ser ajustado mudando o tamanho do bloco. Quanto maior a dimensão vertical mantendo as horizontais constantes maior o ângulo de talude da cava final.

 

Módulo do Geokrige

O Módulo de Cava Ótima que está sendo desenvolvido para o Geokrige utiliza um algoritmo que obtém os mesmos resultados de um Lerchs-Grossmann, porém é mais eficiente em processamento e, com auxílio de artifícios, é capaz de gerar cavas com ângulos de talude constantes em todas as direções ou, se o usuário precisar, ângulos de talude variáveis, para atender à jazidas que possuem condições de estabilidade diferentes em cada região ou direção. O algoritmo usado no Módulo de Cava Ótima do Geokrige será detalhado nos próximos artigos.

 

REFERÊNCIAS

HUSTRULID, William; KUCHTA, Mark; MARTIN, Randall K. Open Pit Mine : Planning and Design. 3ª edição, 2006.