Neste tutorial, vamos ilustrar como calcular um variograma experimental assumindo a existência de anisotropia na área de interesse, usando o pacote gstat.
Inicialmente, a análise exploratória geoestatística comumente é calculada para quatro direções (0º, 45º, 90º, 135º), que formam dois pares ortogonais. Se há anisotropia na área de estudo, o variograma experimental é recalculado na direção de maior continuidade, ou menor variância espacial, e sua direção ortogonal (ver figura 2).
O que é variograma
O variograma é o coração da geoestatística. A função variogram é definida como a esperança matemática do quadrado da diferença entre os valores de pontos no espaço, separados por uma distância, e dada pela a seguinte expressão:
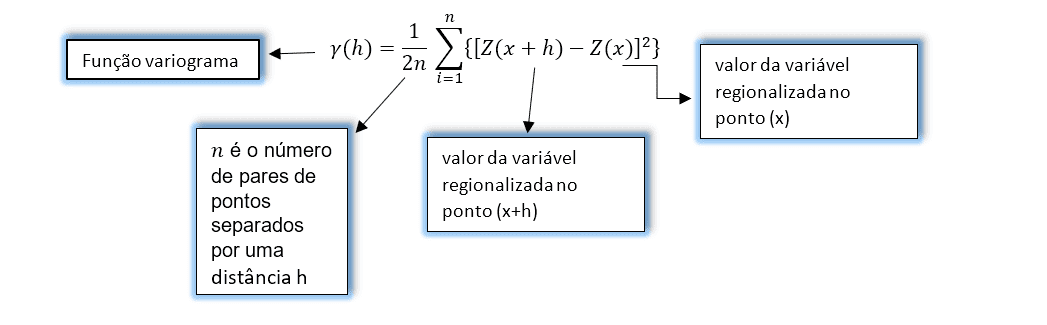
As propriedades do variograma serão ilustradas na Fig.1.

Anisotropia
O fenômeno espacial apresenta anisotropia quando a variação espacial é diferente nas distintas direções do espaço e é geometricamente representada por uma elipse 2D.
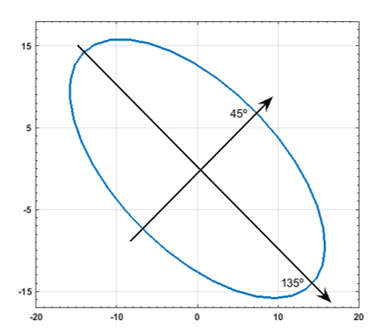
Existem diferentes tipos de anisotropia. As mais comuns encontrados na natureza são: Anistropia Zonal, Geométrica e Mista. Para maior informação procurar na literatura: Yamamoto & Landim (2012, p. 43-44).
Variograma experimental
Os dados utilizados nesta lição serão jura.pred do pacote gstat e mostraremos como este gráfico pode ser personalizado no pacote ggplot2. Para calcular o variograma experimental, usaremos a função variogram() do pacote gstat e usaremos os argumentos:
(object,cutoff,width=cutoff/15,alpha,tol.hor=90/length(alpha))
Cutoff: Distância de separação espacial
Width: Distância mínima entre pontos
Alpha: Direção no plano (x, y) norte = 0º, leste= 90º
O pacote gstat, por defalult, usa um terço da maior diagonal da caixa delimitadora (ou cubo) dos dados na definição do campo geométrico. Para o passo, gstat usa por padrão o campo geométrico dividido por 15.


Pacote ggplot2
Usando as funções observadas em lições anteriores do pacote ggplot2, personalizamos o variograma experimental.


Interessado por geoestatística? Haverá um curso sobre seus fundamentos:


Deixe um comentário
Você precisa fazer o login para publicar um comentário.