Sistemas de Equações Lineares

Os métodos de interpolação para dados 2D ou 3D comumente aplicados nas geociências implicam na resolução de sistemas lineares, cujas dimensões podem ser da ordem de até 12 até milhares de pontos. São exemplos de algumas aplicações: equações multiquádricas, todos os tipos de krigagem (média, simples, ordinária, indicadora, lognormal e multiGaussiana).

Assim, a primeira providência consiste em ter à disposição um eficiente algoritmo para resolução de sistemas lineares. Este artigo faz a introdução do problema, que será seguido por mais dois artigos referentes à resolução de sistemas lineares: método de triangularização de Gauss e método iterativo de Gauss Seidel.

Esses artigos serão acompanhados dos respectivos scripts em R, refletindo a nova orientação da Geokrigagem no sentido de utilizar plataformas open source para o desenvolvimento de seus algoritmos. Evidentemente, a linguagem R proporciona a função solve(), extremamente eficiente e confiável, mas o objetivo de nossas publicações é justamente demonstrar como se aplica a teoria na prática, por meio da programação em R.

O Leitor poderá verificar em nossos scripts a conexão entre a fundamentação teórica e a programação envolvida. Além disso, como o script é aberto, o Leitor poderá fazer modificações para processamentos específicos e, com isso, escrever seus próprios scripts.

Um sistema de equações lineares pode ser visto como (Press et al. 1989, p. 27):

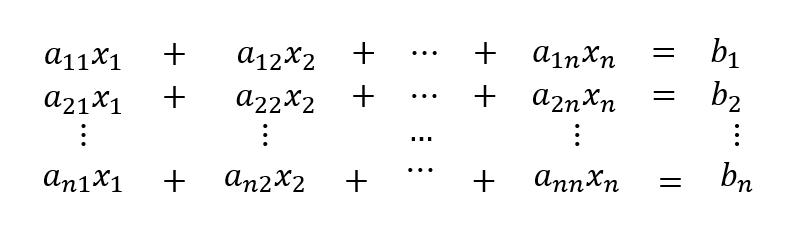
O sistema de equações (1) pode ser escrito na forma matricial (Press et al. 1989, p. 28):

Onde A é a matriz dos coeficientes, x é o vetor das incógnitas e b é conhecido como vetor y. Lembrando que a notação para matrizes usa letras maiúsculas em negrito e para vetores letras minúsculas em negrito, também.

Assim, a solução do sistema de equações lineares envolve a determinação do vetor das incógnitas x.

Encontrando a Solução para as Equações Lineares

Existem diversos métodos para solução de sistemas de equações lineares, que serão apresentados. O Leitor poderá verificar os diversos métodos que fazem manipulação de matrizes, por meio de triangularização, decomposição e extração de autovalores e autovetores. Há também uma solução para sistema de equações homogêneas, ou seja, sistemas singulares que não são passíveis de resolução pelos métodos convencionais.

Uma interpretação geométrica para o sistema de equações lineares pode ser ilustrada para o caso mais simples de duas equações a 2 incógnitas:

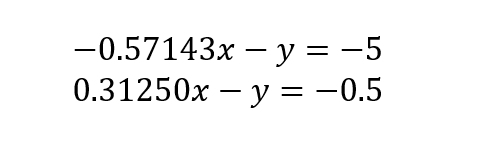
Trata-se de duas retas, em que se procura o ponto de intersecção entre elas, conforme a Figura 1.

Esse sistema pode ser facilmente resolvido pelo método da substituição, conforme segue. Subtraindo-se a segunda da primeira, tem-se:

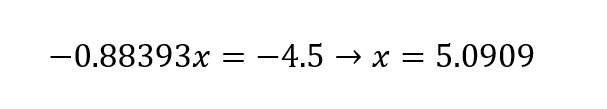
                Substituindo-se o valor de x na segunda, chega-se:

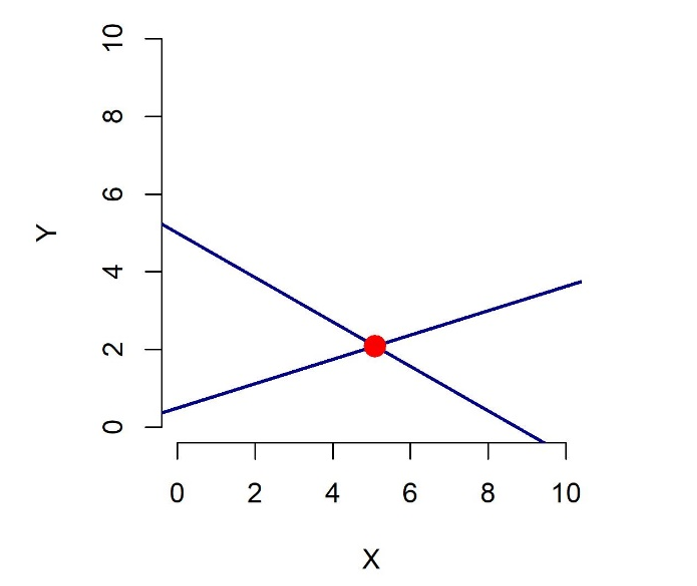
Como se pode ver na Figura 1, a solução é o ponto de intersecção entre as duas retas. Esta figura foi gerada pela execução do script listado a seguir, que faz a representação no dispositivo gráfico do seu computador. Caso queira salvar como jpeg em alta resolução, basta tirar o comentário (#) na frente das linhas respectivas e alterar o diretório em que deseja salvar a figura.

#setwd("C:\\geoStats\\figuras\\testes")
#jpeg("FigRetas.jpeg",width=10,height=10,units="cm",res=300)
par(mar=c(5,5,2,2))
plot(NA,NA,xlim=c(0,10), ylim=c(0,10), type="n", 
frame=FALSE, xlab="X", ylab="Y")
abline(a=0.5,b=0.3125,col="darkblue",lwd=2)
abline(a=5,b=-0.57143,col="darkblue",lwd=2)
points(5.0909,2.0909,pch=21,bg="red",col="red",cex=1.75)
#dev.off()

Próximos artigos

Os dois próximos artigos apresentarão os métodos direto e indireto de resolução de sistemas lineares: triangularização de Gauss e Gauss Seidel. Entretanto, antes desses, vamos publicar um artigo denominado “Gerador de sistemas lineares com script em R”, que tem por objetivo produzir sistemas lineares de quaisquer dimensões, cujas soluções são conhecidas de antemão.

Observação: este artigo foi derivado de um capítulo de um livro em preparação.

Clique aqui e confira nossos livros.

Yamamoto, J.K. 2020. R na prática. São Paulo, JK Yamamoto-EIRELI.