Neste artigo, vamos descrever o método iterativo de Gauss Seidel para resolução de sistemas lineares. Trata-se de um método indireto que converge para a solução dentro de uma tolerância especificada, se a matriz dos coeficientes for estritamente diagonal dominante. Este método consiste em resolver o sistema de equações lineares:
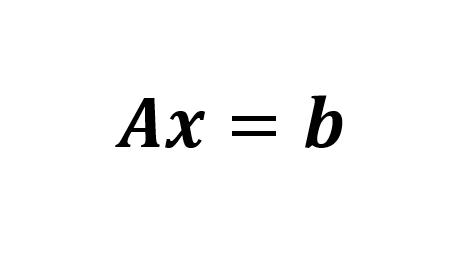
O método faz a partição da matriz dos coeficientes A em L (estrita matriz triangular inferior), D (matriz diagonal) e U (estrita matriz triangular superior), de acordo com Venkateshan e Swaminathan (2014, p. 87):

Isso significa que a matriz dos coeficientes é o resultado da soma de matrizes:
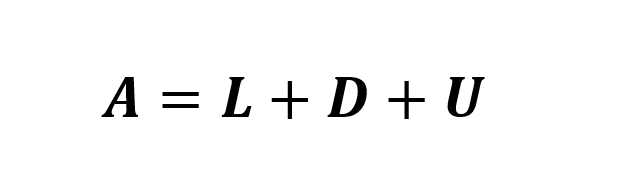
Substituindo-se (2) em (1), chega-se:
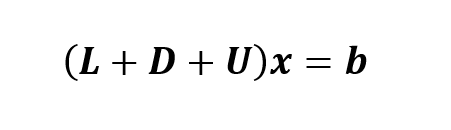
Esta equação pode ser reescrita como (Venkateshan e Swaminathan, 2014, p. 87):

Que pode ser expressa da seguinte maneira, segundo esses autores:

Segundo Venkateshan e Swaminathan (2014, p. 87), esta forma permite a solução pelo processo iterativo, como segue:
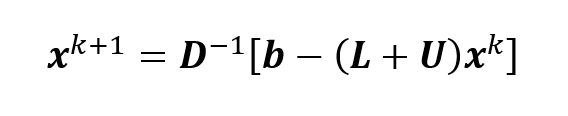
No processo iterativo, a (k+1)-ésima iteração é baseada no resultado da k-ésima iteração. A inversa de uma matriz diagonal é simplesmente o valor recíproco do elemento da diagonal principal. O sistema de equações (3) pode ser escrito como (Venkateshan e Swaminathan, 2014, p. 88):

Trata-se do processo iterativo de Jacobi, onde a iteração para quando a variação para 1 ≤i ≤n (Venkateshan e Swaminathan, 2014, p. 88).
Na verdade, a fórmula (4) não está correta, pois a segunda somatória que começa com (i+1) ultrapassa o limite da matriz quando i for n, j pode ser (n+1).
Exemplo numérico do processo iterativo de Gauss Seidel
Como exemplo numérico, considere-se o exemplo utilizado no nosso artigo “Sistemas de equações lineares”:

A matriz dos coeficientes A é decomposta:
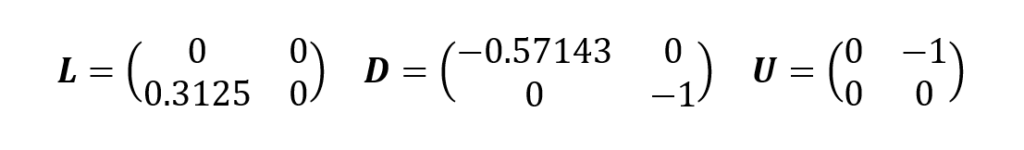
O processo iterativo começa com um chute inicial da solução. Assim, por exemplo, pode-se começar fazendo:

O sistema de equações lineares escrito na forma matricial é:

Substituindo x’ na equação matricial, tem-se:

Evidentemente, b’ não é a solução correta e, por isso, tem-se uma diferença entre o vetor b original e o vetor b’ do chute inicial, que é denominado vetor res (resíduo):

Substituindo-se (6) em (7), tem-se:

O erro é definido como o produto escalar (Venkateshan e Swaminathan, 2014, p. 89):

O erro é muito alto, pois é o resultado do chute inicial. Assim, estabelece-se uma tolerância para o processo iterativo, de tal forma que enquanto o erro for maior que a tolerância, repete-se o processo iterativo. Pode-se definir uma tolerância, nesse caso igual a 0,0001. Considerando o chute inicial como sendo a iteração zero, a primeira iteração é obtida pela expressão (3):

Resolvendo (L+U)xk:
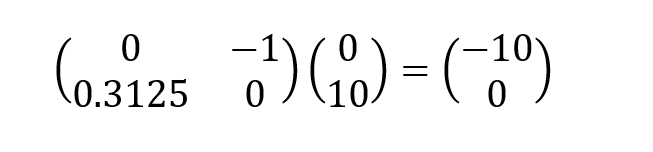
Calculando (b-(L+U)xk), tem-se:

Por fim, determina-se o vetor solução correspondente à primeira iteração:
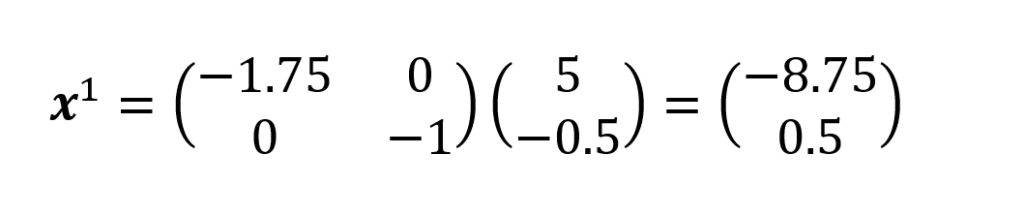
O vetor de resíduos:

Calcula-se o erro como o produto escalar do vetor de resíduos:
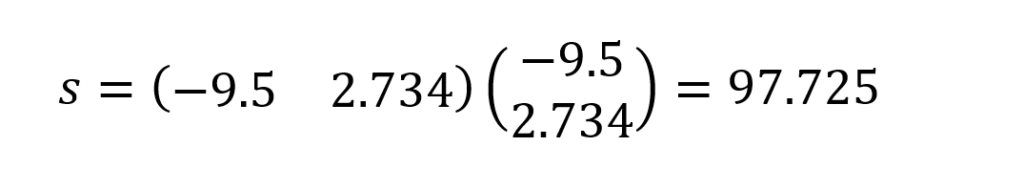
Como o erro é maior que a tolerância, repete-se o procedimento se aplicando (8), (9) e (10), de acordo com os resultados da Tabela 1.
Tabela 1: Resultados do processo iterativo de Gauss Seidel.
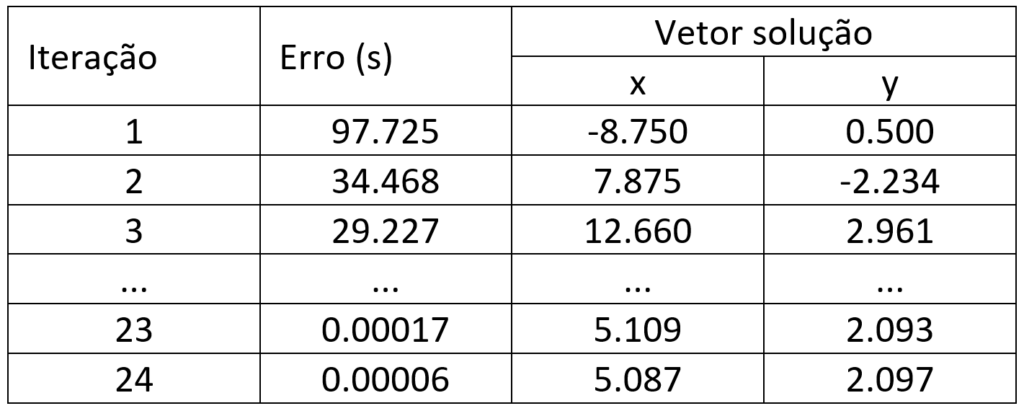
Como se pode verificar, foram necessárias 24 iterações para o erro ser menor que a tolerância (0.0001). Pode-se diminuir a tolerância e, consequentemente, o erro. Porém, este exemplo teve por objetivo ilustrar com uma aplicação numérica o método de iterativo de Gauss Seidel. Nesse caso, houve convergência para a tolerância definida inicialmente. Nesse exemplo, a matriz dos coeficientes apresenta apenas um elemento da diagonal maior que o elemento da linha, em termos absolutos. Entretanto, nem sempre a convergência é possível, pois depende de a condição da matriz dos coeficientes ser estritamente diagonal dominante.
Referência bibliográfica
Venkateshan, S.P.; Swaminathan, P. 2014. Computational methods in engineering. Waltham, Academic Press. 672p.
Próximos artigos
Os próximos artigos em continuidade tratarão da programação em linguagem R do método iterativo de Gauss Seidel, bem como a discussão sobre as condições para convergência desse método.

Deixe um comentário
Você precisa fazer o login para publicar um comentário.